Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học
Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic quốc gia hoặc quốc tế. Tuy nhiên, vinh quang, niềm tự hào này mỗi năm chỉ dành cho một vài thành viên xuất sắc của mỗi quốc gia. Thế nhưng kho tàng kiến thức trong những kì thi đó lại vô cùng tuyệt vời, luôn luôn thu hút đông đảo sự quan tâm của giáo viên, học sinh trên toàn thế giới.
Đặc biệt, bất đẳng thức trong các kì thi Olympic có thể coi là "điểm nóng", thường trở thành phần đề tài giành được nhiều lời giải nhất và được thảo luận nhiều nhất trên các diễn đàn cũng như các tạp chí về Toán học.
Cuốn sách gồm những nội dung:
-
Tóm tắt các đề thi Olympic
-
Hướng dẫn và giải các đề thi
-
Mở rộng một số bài toán trong các kì thi Olympic
3.1: Về một bất đẳng thức tam giác trong IMO 1961
3.2: Cảm hứng từ một bài thi vô địch toán Iran
3.3: Về một bài toán Japan MO
3.4: Bài toán IMO 2001 và những kết quả thú vị
3.5: Bài toán Russia MO và những ý tưởng sáng tạo độc đáo
3.6: Về một bất đẳng thức thú vị
3.7: Những bất đẳng thức kì lạ
Listen Up Plus 3 Student Book (New Edition)
1. Nghệ Thuật Tư Duy Chiến Lược Có phải những người chiến thắng các chương trình truyền hình thực tế được trời phú cho trí thông minh và kỹ năng hơn người? Có phải các
Thuận Theo Hoàn Cảnh - Không Có Một Chiến Lược Phát Triển Vạn Năng Quản trị tốt chính là mục tiêu tối hậu mà mọi quốc gia đều hướng tới trong quá trình phát triển.
Học Toán Qua Trò Chơi Kiểu Nhật - Hình Dạng - Theo PISA (Chương trình Đánh giá học sinh toàn cầu), trẻ em Nhật Bản đứng thứ hai thế giới về môn Toán. - Theo
Lycoris Recoil 2 (Japanese Edition) - fahasa
Chuyện Hay Sử Việt - Nhà Mạc Và Thời Lê-Trịnh - Đất Nước Phân Li Lịch sử đất nước đã trải qua hàng nghìn năm với biết bao thời khắc huy hoàng và bi tráng.
Tokyo Aliens 5 (Japanese Edition) - fahasa
Bài lủng củng, câu văn lắm thì, là, mà quá”. Phê thế đúng, nhưng thật ra cũng chỉ đúng một phần, bởi rất nhiều trường hợp không thể thay thì, là, mà bằng một từ
Ốp hõm và tay nắm cửa cho xe Outlander Chén cửa, một chi tiết của xe rất dễ bị trầy xước do móng tay mỗi khi ta mở cửa xe, thường chúng ta rất ít
With A Mind To Kill Internationally bestselling author Anthony Horowitz’s third James Bond novel, after Forever and a Day. It is M's funeral. One man is missing from the graveside: the traitor who pulled the
" Dracula" là một cuốn tiểu thuyết kinh dị gothic năm 1897 của tác giả người Ireland Bram Stoker , nổi tiếng với nhân vật ma cà rồng bá tước Dracula . Cuốn tiểu thuyết
Ehon Bé Ngoan - Chơi Trốn Tìm Nào Trốn tìm là trò chơi yêu thích của mọi đứa trẻ, nó không chỉ mang tính giải trí mà còn gắn kết người chơi với nhau. Cảm
Bài Tập Ngữ Văn 7 - Tập 2 (Cánh Diều) (Chuẩn)
Haimura Moroha bước vào niên học đầu tiên tại Học viện Akane, ngôi trường đặc biệt chuyên đào tạo "Đấng Cứu Thế" - những học sinh mang kí ức tiền kiếp của các anh hùng
Bộ sách ehon "Điều kỳ diệu của những hình khối" đem đến sự lựa chọn phù hợp cho bố mẹ khi vừa cho con cơ hội tiếp xúc với sách ngay trong độ tuổi từ
👁️
0 | ⌚2025-09-12 22:00:06.507
VNĐ: 138,750
Mua hàng tại Shopee giảm thêm 30%





Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic
Combo Sử Dụng Phương Pháp AM - GM Để Chứng Minh Bất Đẳng Thức + Sử Dụng Phương Pháp Cauchy Schwarz Để Chứng Minh Bất Đẳng Thức + Vẻ Đẹp Bất Đẳng Thức Trong Các
Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic
Combo Sử Dụng Phương Pháp AM - GM Để Chứng Minh Bất Đẳng Thức + Sử Dụng Phương Pháp Cauchy Schwarz Để Chứng Minh Bất Đẳng Thức + Vẻ Đẹp Bất Đẳng Thức Trong Các
Combo 3 cuốn Ám Ảnh Ăn Sạch + Dinh Dưỡng Xanh + Nhân Tố Enzyme - Phương Thức Sống Lành Mạnh ( Bộ sách hay về kiến thức chăm sóc sức khỏe) 1,Ám Ảnh Ăn
Buổi sáng, bạn hãy ôn lại từ mới trong Flash card theo công thức \”Hôm qua, hôm kia và một tuần trước\”: -Lấy các tập Flash card bạn đã làm trong ngày hôm qua, hôm
Tạm Biệt Tôi Của Nhiều Năm Về Trước Nhà xuất bản : Nhà Xuất Bản Dân Trí. Công ty phát hành : Skybooks. Tác giả : An. Kích thước : 13 x 18 cm. Số
Đêm hè năm Chiêu Hòa thứ 25, chàng thanh niên Shiozawa Raichi với sứ mệnh làm gia sư cho tiểu thư một gia tộc quyền thế đã ghé thăm ngôi làng. Ở đó, hình ảnh
Combo 2 Cuốn Sách Nuôi Dạy Con Hoàn Hảo Cho Các Bà Mẹ: Khí Chất Single Mom + Để Con Được Ốm (Tái Bản 2018) / Sách Làm Cha Mẹ Tuyệt Vời Nhất (Tặng Kèm
Bí mật thiêu đốt tâm can (nguyên tác tiếng Đức: Brennendes Geheimnis; tiếng Anh: Burning Secret) từng được các đạo diễn Richus Gliese, Robert Siodmak, Andrew Birkin… chuyển thể thành kịch câm, phim điện ảnh.
Lấy nước đường xa - Cuốn tiểu thuyết dựa trên một câu chuyện có thật tại Châu Phi. Hai câu chuyện đan xen nhau kể về hai đứa trẻ tại Sudan – sống ở hai
Với tốc độ ảnh hưởng của nền văn hóa Hàn Quốc đến Việt Nam hiện nay, tiếng Hàn đang ngày càng trở thành mối quan tâm và là công cụ cho nhiều người muốn tìm
Đây là một cuốn sách sâu sắc và thú vị, giúp bạn đọc khám phá triết học thông qua các câu hỏi kích thích tư duy. Sách chia ra nhiều phần nhỏ, đi từ lý
GÃ HỀ MA QUÁI (TẬP 2) Derry, một thị trấn nhỏ ở Maine, một nơi quen thuộc đến ám ảnh. Chỉ ở Derry, ám ảnh là có thật. Một câu chuyện về bảy người lớn
Tác giả: Ray Bradbury Dịch giả: Lê Hồng Vân Nhà xuất bản: Văn học Số trang: 402 Kích thước: 14x20,5 cm Ngày phát hành: 08-2023 Giới thiệu sách Dẫu được tôn vinh vào hàng kinh
Dòng sách tương tác lật mở vốn được thiết kế để dành riêng cho trẻ trong độ tuổi 0-6 bởi khi đọc, bé được kết hợp các giác quan khác nhau và tư do thao
Đáp ứng nhu cầu ngày càng tăng trong việc tìm hiểu về cổ phần, cổ phiếu, chứng khoán, chiến lược đầu tư của độc giả, Alpha Books chọn mua bản quyền dịch và xuất bản
Kỵ Và Hợp Trong Ăn Uống Trong cuộc sống có quá nhiều cái ăn, nhưng ăn như thế nào cho tốt, ăn vào thời điểm nào và kết hợp những món đó ra làm sao?
Chất liệu tuyệt đối cho sức khỏe Nồi cơm điện tử Elmich 1,8L RCE-1790 có lòng nồi được làm từ nhôm nguyên chất, sử dụng chất chống dính cao cấp của Whitford (Hoa Kỳ) tuyệt
Bộ sách Ehon Kể Chuyện Tuti - Tuti kể về các hoạt động bình thường của bé như "tè dầm", nhưng với một câu chuyện thú vị và độc đáo hơn. Các bé sẽ được
- Compa Mten Thiên Long TP - C012 (Màu Ngẫu Nhiên) có thiết kế nhỏ gọn, giúp bạn vẽ những đường cong hình học khác nhau như: hình tròn, oval, xoắn ố một cách đơn
“Phép so sánh diệu kỳ” là bộ sách Ehon gồm 3 cuốn “To nhỏ”; “Cao thấp”; “Dài ngắn”. Bộ sách là những mẩu chuyện vui về chú Tôm Nhỏ thông thái học cách so sánh
Lý Thuyết Về Hành Động Tương Giao (Bìa Cứng) Lý thuyết về hành động tương giao (Theorie des kommunikativen Handelns), hai tập, 1981, tác phẩm chính của Jürgen Habermas (1929 - ), “triết gia Đức
Rập được in từ giấy A0 , đã được may thử rập. Rập dành cho vải lanh Dành cho các bạn không biết vẽ, cắt vẫn có thể may cho mình những bộ đồ thật
Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic
Combo Sử Dụng Phương Pháp AM - GM Để Chứng Minh Bất Đẳng Thức + Sử Dụng Phương Pháp Cauchy Schwarz Để Chứng Minh Bất Đẳng Thức + Vẻ Đẹp Bất Đẳng Thức Trong Các
Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic
Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic
Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học Nếu yêu thích Toán học, chắc hẳn bạn sẽ không dưới một lần ước mơ mình được tham gia vào đội tuyển Olympic
Combo Sử Dụng Phương Pháp AM - GM Để Chứng Minh Bất Đẳng Thức + Sử Dụng Phương Pháp Cauchy Schwarz Để Chứng Minh Bất Đẳng Thức + Vẻ Đẹp Bất Đẳng Thức Trong Các
Bài này nói về từ điển các chủ đề trong toán học. ## 0-9 * -0 * 0 * 6174 ## A * AES * ARCH * ARMA * Ada Lovelace * Adrien-Marie Legendre *
**Trường Trung học phổ thông chuyên, Đại học Sư phạm Hà Nội** (), tiền thân là Khối Trung học phổ thông chuyên Toán–Tin của Trường Đại học Sư phạm Hà Nội, thường gọi là **Chuyên
**Trường Trung học phổ thông chuyên Hà Nội – Amsterdam** () hay còn được gọi đơn giản là **Trường Ams** là một trường trung học phổ thông công lập của thành phố Hà Nội được
**Trường Trung học phổ thông Chuyên Hà Tĩnh** là trường trung học phổ thông công lập của tỉnh Hà Tĩnh được thành lập từ năm 1991. Đây là trường chuyên duy nhất tại tỉnh Hà
Dưới đây là danh sách các nhân vật trong bộ tiểu thuyết _Chạng vạng_ tác giả Stephenie Meyer, xuất hiện trong Chạng vạng, Trăng non, Nhật thực và Hừng Đông ## Chú giải * Những
**Trường Đại học Dartmouth** (tiếng Anh: _Dartmouth College_; thường gọi là _Dartmouth_, phát âm ) là một đại học nghiên cứu tư thục 254 năm tuổi thuộc nhóm Ivy League danh giá nhất Hoa Kỳ,
**Trường Trung học phổ thông Chuyên Trần Phú** là ngôi trường trung học phổ thông chuyên duy nhất ở Hải Phòng. Trường được thành lập vào tháng 1 năm 1986. ## Lịch sử Trường THPT
**Trường Trung học phổ thông chuyên Nguyễn Quang Diêu** (có tên tiếng Anh là: _Nguyen Quang Dieu High School for the Gifted_) là một trường Trung học phổ thông chuyên công lập tọa lạc tại
**Nam Định** là một tỉnh cũ nằm ở phía Nam Đồng bằng sông Hồng, Việt Nam. Năm 2023, Nam Định là đơn vị hành chính Việt Nam đứng thứ 13 về số dân, xếp thứ
**Đại học Georgia** (, viết tắt là **UGA** hoặc **Georgia**) là một đại học nghiên cứu công lập được cấp đất tại Hoa Kỳ, được thành lập từ năm 1785, có khuôn viên chính ở
:_Bài này nói về Trường Trung học Phổ thông Chuyên Bến Tre tại Bến Tre, ngoài ra còn có Trường Trung học Phổ thông Bến Tre tại Vĩnh Phúc, xem thêm Trường Trung học Phổ
**Văn học Nhật Bản** là một trong những nền văn học dân tộc lâu đời nhất và giàu có nhất thế giới nảy sinh trong môi trường nhân dân rộng lớn từ thuở bình minh
thumb|right|[[Bóng đá là một môn thể thao đồng đội giúp nâng cao sức khỏe và trau dồi các kĩ năng xã hội như tinh thần đồng đội, sự đoàn kết,....]] **Thể thao** (Tiếng Anh: _sport_)
**Thái Bình** là một tỉnh cũ ven biển thuộc vùng đồng bằng sông Hồng. Theo quy hoạch phát triển kinh tế, Thái Bình thuộc vùng duyên hải Bắc Bộ. Theo cuộc Tổng điều tra dân
**Fidel Castro** (tên khai sinh: **Fidel Alejandro Castro Ruz**; ; 13 tháng 8 năm 1926 – 25 tháng 11 năm 2016) là một nhà cách mạng và chính khách người Cuba. Ông là lãnh tụ
**Phạm Thị Huệ** (sinh năm 1996) là một nữ vận động viên điền kinh người Việt Nam. ## Tiểu sử Phạm Thị Huệ sinh ngày 26 tháng 9 năm 1996 tại thôn Tân Lương xã
Combo 3 cuốn Ám Ảnh Ăn Sạch + Dinh Dưỡng Xanh + Nhân Tố Enzyme - Phương Thức Sống Lành Mạnh ( Bộ sách hay về kiến thức chăm sóc sức khỏe) 1,Ám Ảnh Ăn
**Thế vận hội** hay **Olympic** , còn có tên gọi cũ là _Thế giới vận động hội_, là cuộc tranh tài trong nhiều môn thể thao giữa các quốc gia trên toàn thế giới. Thế
là vận động viên trượt băng nghệ thuật chuyên nghiệp và cựu vận động viên trượt băng nghệ thuật cạnh tranh người Nhật Bản thi đấu ở hạng mục đơn nam. Anh là nhà vô
nhỏ|phải|Một kỵ mã [[Mông Cổ với kỹ thuật truyền thống]] **Môn cưỡi ngựa** (_Equestrianism_) hoặc đơn giản là **cưỡi ngựa** (_Horse riding_) hay còn gọi là **mã thuật** hay "thừa mã" là một môn thể
**Rafael Nadal Parera** (, sinh ngày 3 tháng 6 năm 1986 tại Manacor, Mallorca), biệt danh **Rafa**, là một cựu vận động viên quần vợt chuyên nghiệp người Tây Ban Nha. Nadal được đánh giá
**Tập Cận Bình** (giản thể: 习近平; phồn thể: 習近平; bính âm: _Xí Jìnpíng_; phát âm: [ɕǐ tɕînpʰǐŋ], sinh ngày 15 tháng 6 năm 1953) là một chính trị gia người Trung Quốc. Ông hiện đang
**Seattle** (, ) là một thành phố cảng biển tọa lạc ở vùng Tây Bắc Thái Bình Dương của Hoa Kỳ. Thành phố này nằm ở phía tây tiểu bang Washington trên một dải đất
**Hy Lạp**, quốc hiệu là **Cộng hòa Hy Lạp**, là một quốc gia nằm ở phía nam bán đảo Balkan, giáp với Albania, Bắc Macedonia và Bulgaria về phía bắc, Thổ Nhĩ Kỳ và biển
**Ukraina** (phát âm tiếng Việt: _U-crai-na_; , ) là một quốc gia thuộc khu vực Đông Âu, giáp với Nga về phía Đông, Belarus về phía Bắc, Ba Lan, Slovakia và Hungary về phía Tây,
**_Titanic_** là chiếc tàu vượt đại dương chở khách chạy bằng động cơ hơi nước đã đi vào lịch sử ngành hàng hải vì vụ tai nạn hàng hải đã xảy ra với nó
**Istanbul** ( hoặc ; ), là thành phố lớn nhất, đồng thời là trung tâm kinh tế, văn hóa và lịch sử của Thổ Nhĩ Kỳ. Với dân số hơn 14 triệu người (2014), Istanbul
**Brisbane** (Phát âm ) là thành phố thủ phủ và là thành phố đông nhất của bang Queensland của Úc. Nó cũng là thành phố lớn thứ ba ở Úc. Nó nằm gần Thái Bình
**Lyon** (phát âm [ljɔ̃]; phiên âm tiếng Việt: **Li-ông**) là thành phố toạ lạc ở phía đông nam nước Pháp, là nơi hợp lưu của hai con sông là sông Rhône và sông Saône. Lyon
**_The Amazing Race 10_** là chương trình thứ 10 của loạt chương trình truyền hình thực tế_The Amazing Race_. _The Amazing Race 10_ bao gồm 12 đội hai người đã quen biết từ trước trong
**Almaty** (; tên trước đây là **Alma-Ata**, cũng gọi là **Verniy**, (Верный)) là thành phố lớn nhất của Kazakhstan với dân số 1.801.713 người, chiếm khoảng 8% tổng dân số cả nước và hơn 2
**Trượt băng nghệ thuật** (tiếng Anh: _figure skating_) là môn thể thao trong đó các cá nhân, đôi hoặc nhóm biểu diễn bằng giày trượt băng trên sân băng. Đây là môn thể thao mùa
**Bảy kỳ quan thiên nhiên của thế giới** (tiếng Anh: New 7 Wonders of Nature) là một cuộc bình chọn do công ty tư nhân New Open World (NOW) Corporation, đặt trụ sở tại Thụy
Dàn nhân vật phụ trong anime/manga **_Hetalia: Axis Powers_** cực kì hùng hậu. Sau đây là những quốc gia hay được nhắc đến nhất ngoài khối Phát xít và Đồng Minh. Phần giới thiệu sẽ
Mùa thứ ba của **_Supermodel po-ukrainsky_** được dựa theo _America's Next Top Model_ của Tyra Banks. Alla Kostromichova, Serhiy Nikityuk, Sonya Plakydyuk và Richard Horn quay lại làm giám khảo cho mùa này. Kể từ
**Angelina Jolie** (; tên khai sinh **Angelina Jolie Voight**; Jolie là em gái của diễn viên James Haven cũng như là cháu gái của ca sĩ kiêm nhạc sĩ Chip Taylor và nhà địa chất
**Buôn Ma Thuột** (còn được viết là **Ban Mê Thuột**) là thành phố tỉnh lỵ cũ của tỉnh Đắk Lắk, Việt Nam. Đây là thành phố lớn nhất ở vùng Tây Nguyên và là đô
Ngày **1 tháng 1** là ngày thứ 1 trong lịch Gregory. Đây là ngày đầu tiên trong năm. ## Lịch sử Trong suốt thời Trung cổ dưới ảnh hưởng của Giáo hội Công giáo Rôma,
**Macedonia** (; ), còn được gọi là **Macedon** (), là một vương quốc cổ đại nằm ở ngoài rìa phía bắc của nền văn minh Hy Lạp Cổ xưa và Hy Lạp Cổ điển, và
**Kang Daniel** (, tên khai sinh **Kang Eui-geon**, sinh ngày 10 tháng 12 năm 1996) là một nam ca sĩ, nhạc sĩ, diễn viên, MC và doanh nhân người Hàn Quốc nổi tiếng vào đầu
**Sokrates** (; , ; phiên âm tiếng Việt: Xô-crát; – 399 TCN) là một triết gia người Hy Lạp cổ đại (người Athens), ông được coi là một trong những người đã sáng tạo ra nền
**Douglas MacArthur** (26 tháng 1 năm 18805 tháng 4 năm 1964) là một nhà lãnh đạo quân sự người Mỹ, từng giữ chức Thống tướng lục quân Hoa Kỳ, cũng như là Thống chế của
Bản đồ Rio de Janeiro, 1895 **Rio de Janeiro** (phát âm IPA ; theo tiếng Bồ Đào Nha nghĩa là "dòng sông của tháng Giêng"), hay còn gọi tắt là **Rio** là thành phố tại
**Nokia Corporation** (pronunciation ) (, , ) là tập đoàn viễn thông đa quốc gia có trụ sở tại Keilaniemi, Espoo, Phần Lan. Nokia tập trung vào các sản phẩm viễn thông không dây và





 Listen Up Plus 3 Student Book (New Edition)
Listen Up Plus 3 Student Book (New Edition)  Combo 2 Cuốn: Nghệ Thuật Tư Duy Chiến Lược + MBA Căn Bản
Combo 2 Cuốn: Nghệ Thuật Tư Duy Chiến Lược + MBA Căn Bản  Thuận Theo Hoàn Cảnh - Không Có Một Chiến Lược Phát Triển Vạn Năng
Thuận Theo Hoàn Cảnh - Không Có Một Chiến Lược Phát Triển Vạn Năng  Học Toán Qua Trò Chơi Kiểu Nhật - Hình Dạng
Học Toán Qua Trò Chơi Kiểu Nhật - Hình Dạng  Lycoris Recoil 2 (Japanese Edition)
Lycoris Recoil 2 (Japanese Edition)  Chuyện Hay Sử Việt - Nhà Mạc Và Thời Lê-Trịnh - Đất Nước Phân Li
Chuyện Hay Sử Việt - Nhà Mạc Và Thời Lê-Trịnh - Đất Nước Phân Li  Tokyo Aliens 5 (Japanese Edition)
Tokyo Aliens 5 (Japanese Edition)  Tiếng Việt Giàu Đẹp - Nỗi Oan Thì, Là, Mà (Tái Bản 2022)
Tiếng Việt Giàu Đẹp - Nỗi Oan Thì, Là, Mà (Tái Bản 2022)  Ốp hõm và tay nắm cửa cho xe Outlander
Ốp hõm và tay nắm cửa cho xe Outlander  With A Mind To Kill
With A Mind To Kill  Bá Tước Dracula (Tái Bản 2022)
Bá Tước Dracula (Tái Bản 2022)  Ehon Bé Ngoan - Chơi Trốn Tìm Nào (Tái Bản 2022)
Ehon Bé Ngoan - Chơi Trốn Tìm Nào (Tái Bản 2022)  Bài Tập Ngữ Văn 7 - Tập 2 (Cánh Diều) (Chuẩn)
Bài Tập Ngữ Văn 7 - Tập 2 (Cánh Diều) (Chuẩn)  Khúc Nguyền Ca Của Thánh Kiếm Sĩ (Tập 3)
Khúc Nguyền Ca Của Thánh Kiếm Sĩ (Tập 3)  Combo 9 cuốn sách Ehon Điều kỳ diệu của hình khối và Những mẩu chuyện vụn vặt của Maru
Combo 9 cuốn sách Ehon Điều kỳ diệu của hình khối và Những mẩu chuyện vụn vặt của Maru  VẺ ĐẸP BẤT ĐẲNG THỨC TRONG CÁC KÌ THI OLYMPIC TOÁN HỌC - TÁI BẢN
VẺ ĐẸP BẤT ĐẲNG THỨC TRONG CÁC KÌ THI OLYMPIC TOÁN HỌC - TÁI BẢN  Combo Sử Dụng Phương Pháp AM - GM Để Chứng Minh Bất Đẳng Thức + Sử Dụng Phương Pháp Cauchy Schwarz Để Chứng Minh Bất Đẳng Thức + Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học _HA
Combo Sử Dụng Phương Pháp AM - GM Để Chứng Minh Bất Đẳng Thức + Sử Dụng Phương Pháp Cauchy Schwarz Để Chứng Minh Bất Đẳng Thức + Vẻ Đẹp Bất Đẳng Thức Trong Các Kì Thi Olympic Toán Học _HA  Sách Tham Khảo- Combo Sử Dụng Phương Pháp AM-GM +Sử Dụng Phương Pháp Cauchy Schwarz+Vẻ Đẹp Của Bất Đẳng Thức(3 Cuốn)- HA
Sách Tham Khảo- Combo Sử Dụng Phương Pháp AM-GM +Sử Dụng Phương Pháp Cauchy Schwarz+Vẻ Đẹp Của Bất Đẳng Thức(3 Cuốn)- HA  Combo 3 cuốn Ám Ảnh Ăn Sạch + Dinh Dưỡng Xanh + Nhân Tố Enzyme - Phương Thức Sống Lành Mạnh ( Bộ sách hay về kiến thức chăm sóc sức khỏe)
Combo 3 cuốn Ám Ảnh Ăn Sạch + Dinh Dưỡng Xanh + Nhân Tố Enzyme - Phương Thức Sống Lành Mạnh ( Bộ sách hay về kiến thức chăm sóc sức khỏe)  Thẻ Flashcard - Học Từ Vựng Tiếng Trung Căn Bản
Thẻ Flashcard - Học Từ Vựng Tiếng Trung Căn Bản  Tạm Biệt Tôi Của Nhiều Năm Về Trước
Tạm Biệt Tôi Của Nhiều Năm Về Trước  Gia Sư Của Công Chúa Quỷ
Gia Sư Của Công Chúa Quỷ  Combo 2 Cuốn Sách Nuôi Dạy Con Hoàn Hảo Cho Các Bà Mẹ: Khí Chất Single Mom + Để Con Được Ốm (Tái Bản 2018) / Sách Làm Cha Mẹ Tuyệt Vời Nhất (Tặng Kèm Poster An Toàn Cho Con Yêu)
Combo 2 Cuốn Sách Nuôi Dạy Con Hoàn Hảo Cho Các Bà Mẹ: Khí Chất Single Mom + Để Con Được Ốm (Tái Bản 2018) / Sách Làm Cha Mẹ Tuyệt Vời Nhất (Tặng Kèm Poster An Toàn Cho Con Yêu)  Bí mật thiêu đốt tâm can
Bí mật thiêu đốt tâm can  Lấy Nước Đường Xa + Tặng Kèm Bookmark
Lấy Nước Đường Xa + Tặng Kèm Bookmark  6000 Câu Giao Tiếp Tiếng Hàn Theo Chủ Đề (Tặng kèm Kho Audio Books)
6000 Câu Giao Tiếp Tiếng Hàn Theo Chủ Đề (Tặng kèm Kho Audio Books)  Triết học kỳ thú dành cho tuổi mới lớn
Triết học kỳ thú dành cho tuổi mới lớn  Sách - Biên niên ký sao Hỏa (Nhã Nam HCM)
Sách - Biên niên ký sao Hỏa (Nhã Nam HCM)  Sách Lật Mở Khám Phá - Lift The Flap (Nhiều Chủ Đề ) - Đinh Tị Books
Sách Lật Mở Khám Phá - Lift The Flap (Nhiều Chủ Đề ) - Đinh Tị Books  Trạm Đọc | Chết Vì Chứng Khoán
Trạm Đọc | Chết Vì Chứng Khoán  Kỵ Và Hợp Trong Ăn Uống - FN
Kỵ Và Hợp Trong Ăn Uống - FN  Nến ly Goose Creek (200g) - Tree Cutting
Nến ly Goose Creek (200g) - Tree Cutting  Nồi cơm điện tử Elmich 1,8L RCE-1790 - Hàng chính hãng
Nồi cơm điện tử Elmich 1,8L RCE-1790 - Hàng chính hãng  Ehon Kể Chuyện - Tuti Tuti - Bãi Tè, Roong Roong (Từ 1 - 6 Tuổi)
Ehon Kể Chuyện - Tuti Tuti - Bãi Tè, Roong Roong (Từ 1 - 6 Tuổi)  Compa Mten Thiên Long TP - C012 (Màu Ngẫu Nhiên)
Compa Mten Thiên Long TP - C012 (Màu Ngẫu Nhiên)  Ehon Phép So Sánh Diệu Kỳ - Cao Thấp
Ehon Phép So Sánh Diệu Kỳ - Cao Thấp  Lý Thuyết Về Hành Động Tương Giao (Bìa Cứng)
Lý Thuyết Về Hành Động Tương Giao (Bìa Cứng) 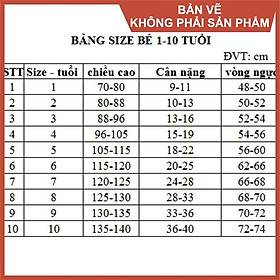 Rập giấy A0 mã R413 (BẢN VẼ)
Rập giấy A0 mã R413 (BẢN VẼ)  VẺ ĐẸP BẤT ĐẲNG THỨC TRONG CÁC KÌ THI OLYMPIC TOÁN HỌC - TÁI BẢN
VẺ ĐẸP BẤT ĐẲNG THỨC TRONG CÁC KÌ THI OLYMPIC TOÁN HỌC - TÁI BẢN